Project information

• Project: Master Thesis - 6 mnoths
• Institution: UBS and PLUS
• Project date : 26 June, 2024
• Project URL: Master Thesis
• Key Skills: Machine Learning, Learning Representation, Remote Sensing, Crop Classification, Deep Learning, Riemannian Geometry

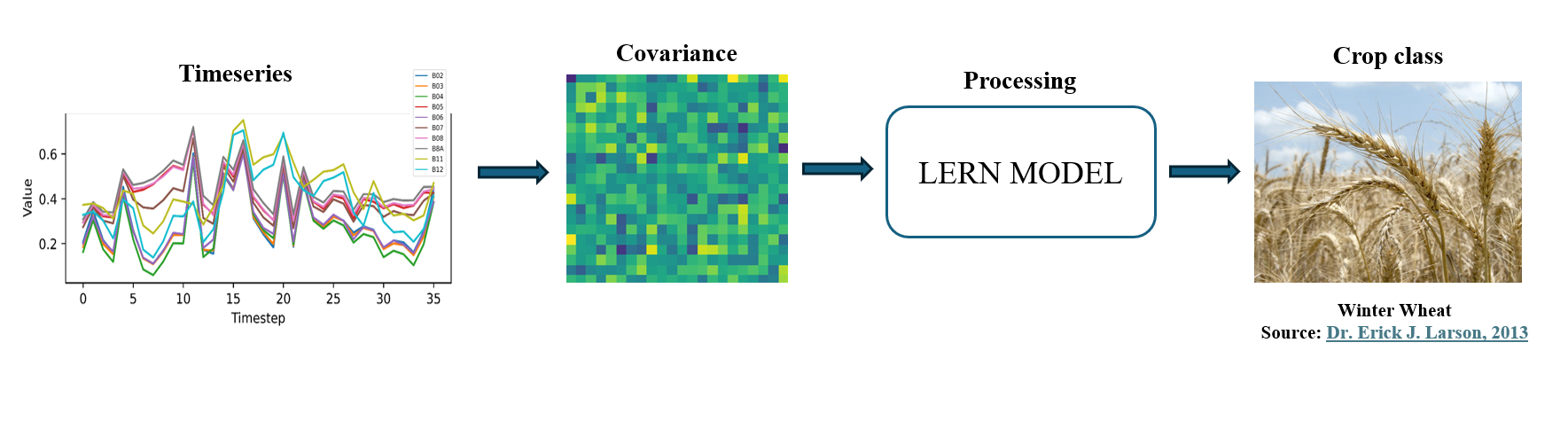
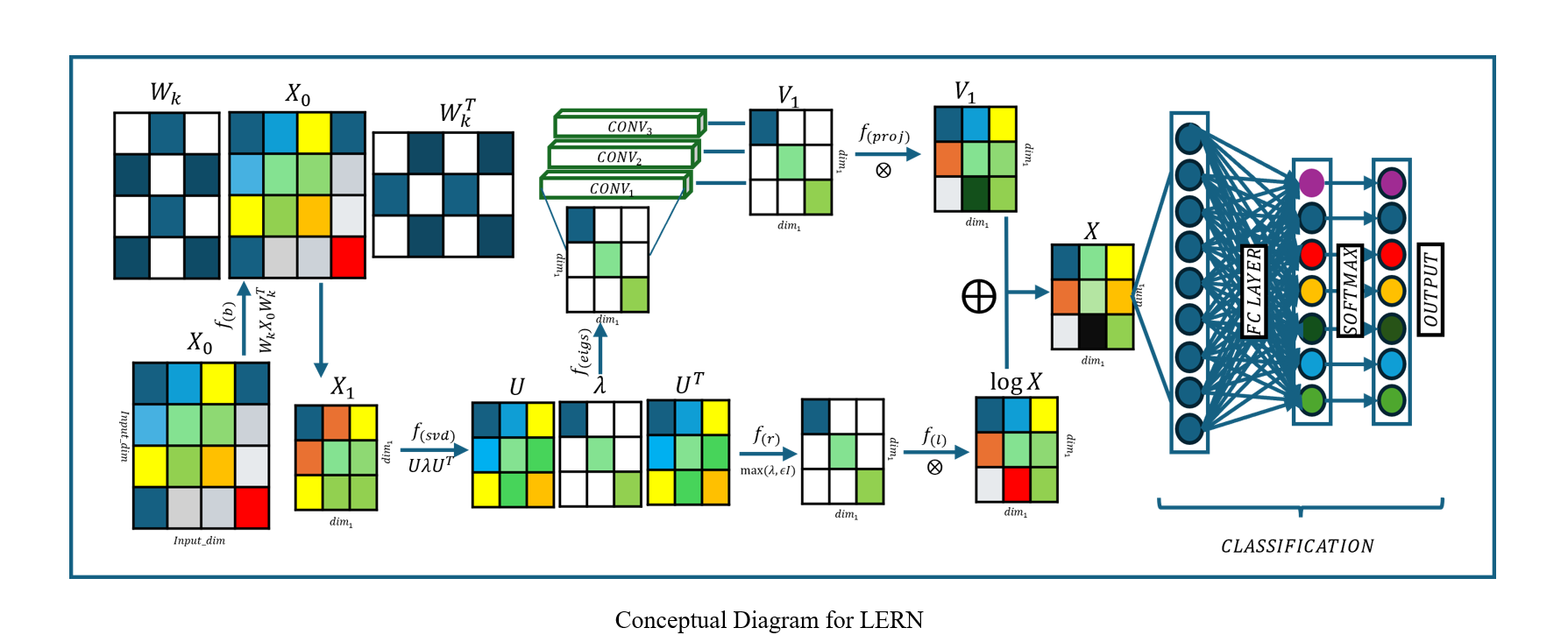
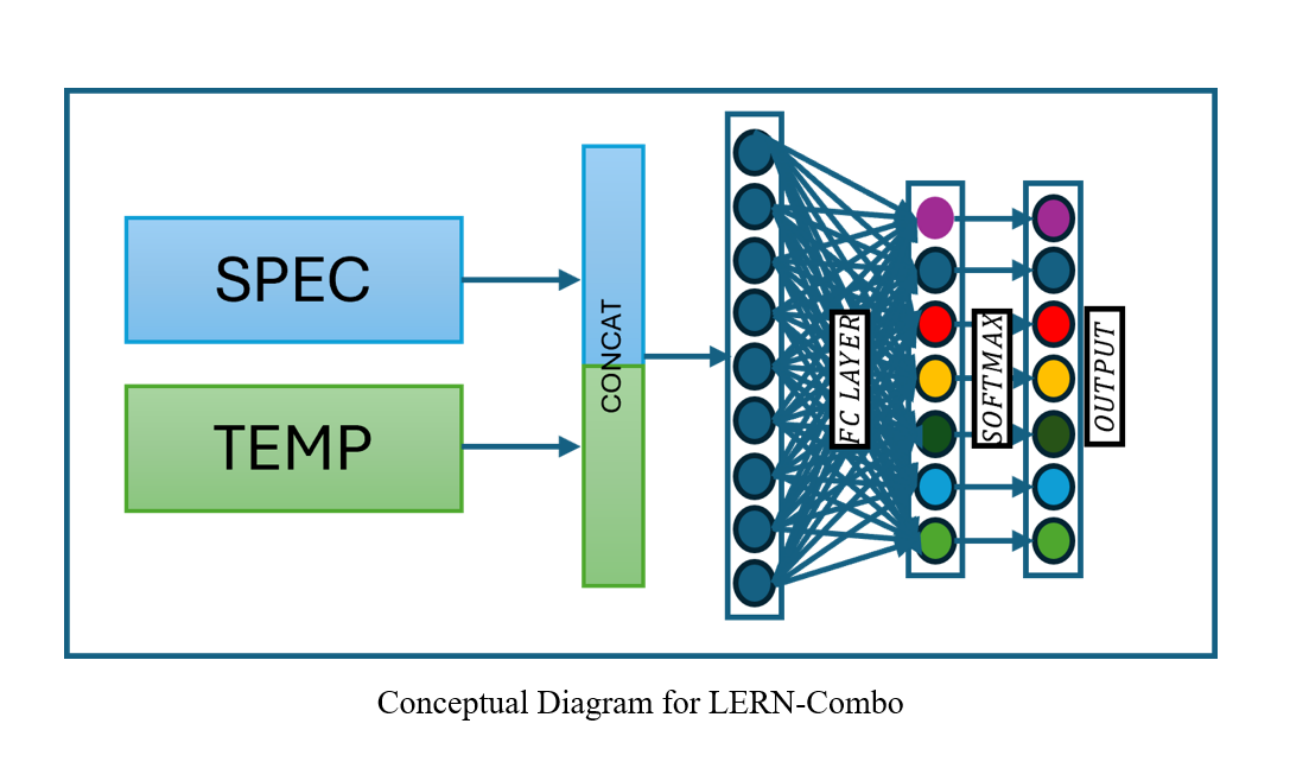
This study explores the application of Symmetric Positive Definite (SPD) matrices on the Riemannian manifold to classify multivariate remote sensing time series data. Remote sensing time series are represented as covariance matrices, capturing statistical dependencies and temporal dynamics. Leveraging this covariance representation and the inherent geometrical structure, this study introduces LogEucResNet (LERN) a second-order geometry-aware neural network designed for crop classification tasks. This work draws inspiration from the success of compact representation of brain signals using covariance matrices in the field of M/EEG signals classification. LERN utilizes concepts from differential geometry and linear algebra to embed covariance matrices onto the Riemannian manifold, facilitating the extraction of latent features crucial for classification. We introduce a novel fusion variant, LERN-Combo in this study. The novel LERN-Combo variant integrates spectral and temporal sub-models, enhancing classification accuracy by capturing both spectral and temporal patterns simultaneously. Evaluation on benchmark datasets such as MiniTimeMatch and BreizhCrops demonstrates superior performance of LERN-Combo and LERN-Temp over LERN-Spec, achieving higher macro-F1 scores. This highlights the effectiveness of second-order statistical representations in capturing intricate dependencies within time series data. This research underscores the efficacy of Riemannian manifold-based approaches in advancing remote sensing classification tasks, contributing significantly to the digital earth observation domain. By introducing a Riemannian network architecture tailored to remote sensing, this study pioneers new directions in non-linear learning of SPD matrices within deep models to exploit the geometric properties of data for improved analysis and classification.